LASSO回归

1、功能介绍

LASSO回归：是在拟合广义线性模型的同时进行变量筛选和复杂度调整。因此，不论因变量是连续的（continuous），还是二元或者多元离散的（discrete），都可以用 LASSO 回归建模然后预测。复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过度拟合

建模的过程就是模型对数据的普遍规律的总结，例如在线性模型中，输入自变量的数值，通过线性公式的转换，让最终得到的因变量的值和实际的因变量的值相差尽量小，这就是模型的拟合过程。LASSO可以有效的避免过拟合

让我们看看下图，从左往右依次是欠拟合，拟合效果良好和过拟合

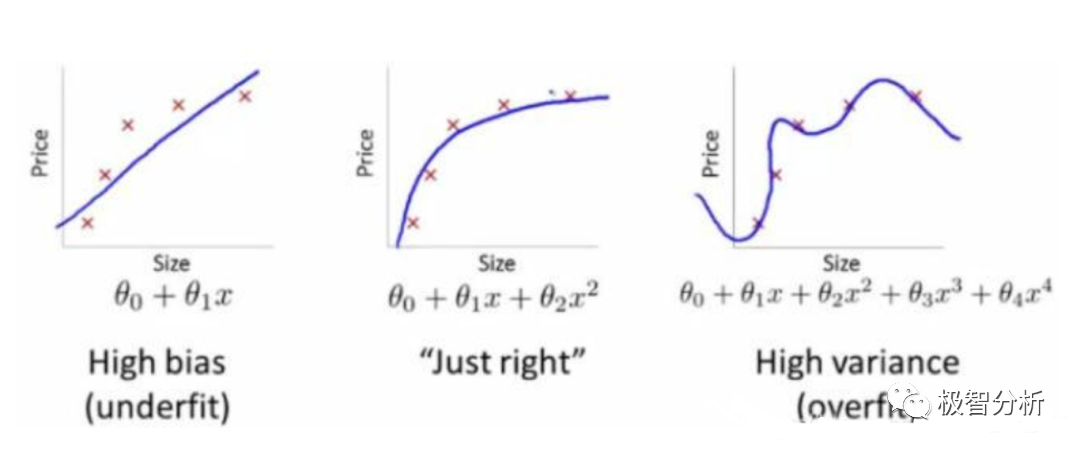
欠拟合：模型没有正确认识到数据体现的普遍规律，无法对作出良好的预测。

过拟合：模型将数据中的全部信息都当做普遍规律，在训练集样本可以达到完美的效果，但用于样本外的测试情况就不行了，因为它可能将一些片面的、只体现于小部分样本的规律误认为是复合总体样本的普遍规律了，这种的模型最终效果也是不好的，我们要避免这两种情况。

2、平台操作

针对要研究的数据，选入因变量和所有自变量，根据研究目标二分类选择binom（连续型因变量选择gaussian、带有时间变量选择cox）。

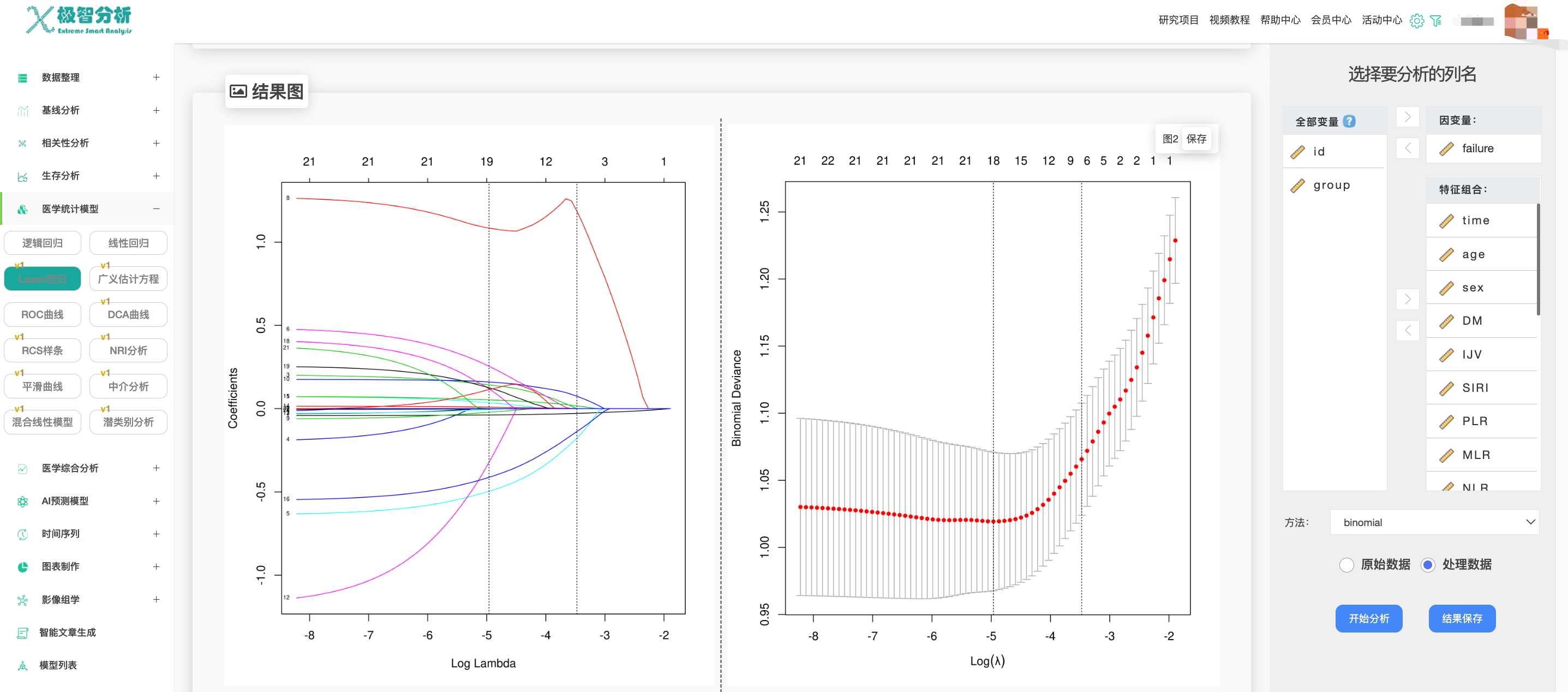
可以看到，右图的垂直虚线对应的最低点的惩罚值（即曲线最低点对应的上坐标），在左图的相应惩罚值的位置寻找对应位置的垂线，相交的点数即为最终模型纳入的变量数目，对应交点的纵坐标即为该变量的回归系数。结果描述中给出了两种惩罚情况下的最佳变量组合。

3、案例分析

以这篇文章于2016年发表在JOURNAL OF CLINICAL ONCOLOGY杂志(IF=44.544)上的，该研究的目的是建立和验证一个放射组学列线图，该列线图结合了放射组学特征和临床病理危险因素，用于大肠癌患者术前预测淋巴结转移。

使用LASSO进行特征选择，根据10倍交叉验证，选择λ值为0.009，log（λ）为24.709，图为150个纹理特征的系数剖面。根据log（λ）序列绘制了系数剖面图。使用10倍交叉验证在选定值处绘制垂直线，其中最佳λ产生24个非零系数。